1. Opste definisanje proporcija
Proporcija se definise kao medjusobni odnos velicina jedne prema drugoj (npr. jedan lik je dvostruko veci od drugoga, drugi je trostruko manji od trecega, jedan je jednak drugome. Odnosi su cisto matematicki. Sto se primera tice to su skulpture i skulptoralna plastika. Tako naprimer kod kopljonose, taj odnos je 1:7 tj. glava se sedam puta sadrzi u telu skulpture. Da bi smo bolje objasnili proporcije koristicemo se jednim primerom matematicke analize. Ako postavimo odnose vise elemenata, npr. mali cekic i dvostruko veci, muzicke tonove C1 i C2 (razmak oktave), dete visoko 90 cm i odraslog coveka visokog 180 cm, te brojeve 13 i 26 tematski izmedju njih necemo naci nista zajednicko, ali vec na drugi pogled uocavamo kako su svi parovi postavljeni u odnose 1:2 (tj. omer dvostruke vrednosti jednog predmeta prema drugom). Tako pocinjemo govoriti o proporcijama tj.razmeru velicina.Na primer, postavili smo u odnos vise omera i vise velicina. Kod razmere je odnos uvek ocuvan. Tako dolazimo do definicije razmera da je on zapravo izjednacavanje omera.
Imamo primer toga: a:b=b:c, dok je brojni primer 1:3=3:9, isto tako a:b=b:(a+b) tzv. zlatni rez (presek) ujedno uocavamo kako za elemente u omeru koristimo znak ":" koji matematicki zovemo deljenje, pa je tako omer elemenata uvek izracunljiv, izmerljiv i postavljen u dalje odnose tj.razmere.
2. Teorije nizova
Iz pravila teorije nizova proizilaze progresivni nizovi brojeva, u kojima se bilo koja 2 susedna broja medjusobno jednako odnose kao bilo koja 2 susedna broja. Najpoznatiji proporcionirani nizovi su:
1. aritmeticki
2. geometrijski
3. harmonijski niz
Pravila zbrajanja nizova su sledeca:
1. aritmeticki niz - uvek se isti broj sabira sa svakim sledecim brojem tj.clanom niza sto cini da se sve velicine izmedju 2 clana jednake uvek npr.,1,2,3,4,5... svaki broj se sabira sa 1 (+1) ili 1,4,7,10....(zbroj sa 3) itd.
2. geometrijski niz- uvek isti broj mnozi se sa svakim sledecim clanom niza,sto cini da se velicine izmedju 2 clana uvek velikom brzinom povecavaju npr. 1,2,4,8,16,32...pomnozeno sa 2, operacija mnozenje
1,3,9,27,81....pomnozeno sa 3 svaki broj, operacija mnozenje.
3. harmonijski niz pocinje od celog broja 1, koji se deli na 1/2,1/3,(ili 2/3),1/4,(ili 3/4),1/5 ili 4/5,1/6 ili 5/6 itd... posto je harmonijski niz zapravo aritmeticki niz pod razlomkom 1,2,3,4...-1,1/2,1/3,1/4) o njemu se govori kao o obrnutoj proporciji. U njemu ce mnogi prepoznati tajnu percepiranja sveta... Pitagora uspostavlja glavne konsonante: 1/2 oktava,2/3 kvinta,3/4 kvarta
3. Primeri iz umetnosti i arhitekture
Leonardo da Vinci ce zapisati kako ono sto se radi u prirodi, u aritmetickom nizu - drvored, vidimo kao harmonijski niz (geometrijska perspektiva). Zbog ovog niza grcki filozof Zenon pobija mogucnost kretanja: ako ispustim kamen iz ruke, pre negoli padne na zemlju mora prvo doci do 1/2 puta:a pre toga do prve trecine, a pre do 1/4, a pre do 1/5...zapravo kaze Zenon, ne moze uopste ni krenuti!
* imamo primer u kompjuterskoj grafici animacije u 3D max programu za arhitekte!
Fibonacijev niz: 2 clana niza zbrojena medjusobno daju sledeceg clana niza 1,1,2,3,5,8,13,21,34...
Odnosi u ovom nizu su u zlatnom preseku: 1,618...
* ovu cinjenicu jos odavno koriste umetnici i arhitekte trazeci u proporcijama i razmerima odraz nacela stvaranja u prirodi, neki zajednicki nazivnik, koji bi bio dokaz traga ruke zajednickog stvaraoca. Najpoznatiji rezultat istrazivanja poznajemo pod imenom ZLATNI REZ, razmer velicina u kome se manji deo odnosi prema vecem kao taj veci prema celini (ukupnom zbiru manjeg i veceg) tako formulom
a:b=b:(a+b)
minor:major=major:celina
1,1,2,3,5,8,13,21,34,55
svaki sledeci jednak je zbiru prethodna 2 broja
4.Istorijat zlatnog preseka u prirodi kao i zlatnog preseka u arhitekturi i umetnosti
Otkrice zlatnog preseka pripisuje se starim Grcima, zbog njihovih zabeleski i instrumenata koje su koristili, ali proporcije zlatnog preseka nalazimo vec na Egipatskim gradjevinama. To je rezultat njihovih astronomskih merenja prirode kojoj je Zlatni presek jedno od osnovnih oblikovnih nacela. Razmera zlatnog preseka izrazena je u Fibonacijevom nizu 1,1,2,3,5,8,13,21,34,55... gde je svaki sledeci broj jednak zbiru prethodna 2 broja. Traganja za savrsenim proporcijama dovelo je umetnike stare Grcke do uspostavljanja kanona odnosno modula, osnovnih mera proporcionalnih gradjevinama. Te teorije su narocito bile razvijene u 18.veku.
Najcesce korisceni odnosi su bili, velicina glave:ostatku tela, tako je kod vajara Polikleta iznosila 1:6, a kod vajara Praksitela 1:7,velicina glave sadrzavala se 6 ili 7 puta u velicini tela.
5. Autori koji su se bavili proporcijama u arhitekturi i umetnosti
Prema istoricaru umetnosti Winkelmann-u, Grci su svoju decu vezbali u crtanju ljudskih tela kako bi naucila gledati i videti proporcionalne odnose i tako stekla smisao za lepo. Modulima se bavio Vitruvije u antici, (10 knjiga o arhitekturi), Leonardo da Vinci u renesansnom periodu i Albreht Direr u 15.veku, (takodje renesansa) zatim Le Korbizje u XX veku...
Ta ista znanja o pravilnim odnosima velicina koriste se i za namerno krsenje pravila posebno u karikaturi (isticanjem smesnih i karakteristicnih elemenata neke osobe) i tzv. naivnom slikarstvu.
Disproporcionalnost je posebno vidljiva u decijem crtezu, gde se semantickom (ikonoloskom) perspektivom naglasavaju vaznije stvari u prikazu (mnogi umetnici su stoga trazili uzore upravo u decijem likovnom izrazu).
6. Proporcionalnost u arhitekturi
Nadalje, proporcionalnost je vazna i u arhitekturi. Jos od stare Grcke poznajemo geslo ``covek je merilo stvari`` sto treba prihvatiti na 2 nivoa:
Prvo, arhitektura ima uvek utilitarno svojstvo---njena funkcija odredjuje njen oblik i mere
primer - to znaci da npr. vrata moraju odgovarati prosecnoj visini osobe koja ce ta vrata koristiti odnosno prolaziti kroz njih. Zljebovi na stubovima grckih hramova, kanelure, imaju sirinu ljudskih ledja, kako bi se osobe koje se okupljaju ispred hrama mogle na njih nasloniti i odmoriti.
Drugo, u projektovanju zgrada koriste se razmeri ljudskih proporcija, cime se stvara osecaj sklada i prihvatanja od strane gledaoca, koji na nesvesnom nivou u odnosima arhitektonskih elemenata prepoznaje odnose vlastitog tela. Ceo stub se, npr. odnosom kapitela i tela stuba odnosi kao ljudska glava prema telu, a razmak izmedju stubova razmeran je rasponu koraka coveka. Posebno je vazno i ovo: rec RAZMER na latinskom se zvala PROPORCIJA, a na grckom ANALOGIJA.
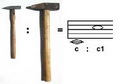
Pitagora, je prema prici prolazeci pored kovacnice cuo zvuke udaranja cekica o nakovanj u oktavama. Usavsi, video je kako su cekici napravljeni u razmeri 1:2, jedan je dvostruko veci od drugog. Time se stvorio, analogan proporcionalan odnos. Manji cekic prema vecem kao nota C prema noti C1! Ta spoznaja omogucila mu je istrazivanje skrivenih odnosa medju stvarima koje je poceo svuda pronalaziti. Stoga je za univerzum skovao naziv kosmos, uredjeni suprotan od haosa. Iz ovih razmisljanja pojavljuju se reci struktura, nadredjeni red i korelacija- slicnost... Kad jedno na drugo lici, po istim nacelima, dakle, ne po temi nego po sadrzaju. Primer imamo, kod skolske nastave, otkrivanjem sakrivanih relacija ucenik i student ne usvaja samo znanje vec i odusevljenje u posmatranju i istrazivanju.
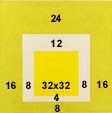
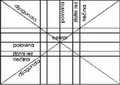
Proporcionalnost je od izuzetne vaznosti pri konstruisanju kompozicija u slikarstvu. To znaci da se vec sam format platna ili papira pazljivo odredjuje odnosom h prema b=sirina. Najpoznatiji je takozvani AURON, zlatni pravougaonik, kome su stranice u odnosu zlatnog reza, ali format moze biti dvostruki kvadrat u promatranju i istrazivanju. Svaki format ima u sebi rasporedjene nevidljive povlascene tacke koje uticu na silnice koje se aktiviraju smestanjem likova na 3 mesta. Najvazniji je svakako, centar (polovina formata V i H) prema kome likovi padaju, lebde, stabilni su i nestabilni. Tu su zatim, trecine, zlatni rezovi i dijagonale, a zatim celi mikrosvet nastaje kombinacijama ovih pravila.
Mesto na kome se seku 2 zlatna reza V i H, nazivamo opticko srediste ( ne mesati sa ocistem u geometrijskoj perspektivi). Veoma vazan deo likovnog izraza cini odabir mesta unutar formata na koja autor smesta pojedine elemente svoje kompozicije.Slikovni primer je slika Pietra Vannucia (Perugina) ``Predaja kljuceva``...